Etiquetas
Actualización: un segundo artículo donde respondo a las cuestiones y errores más frecuentes sobre este tema: Más de CUP, el mal uso de probabilidades y un bayesiano.
En Twitter preguntan cuál era la probabilidad de empate:
Dado que había ya respuestas erróneas respondí, luego expliqué cuál es la forma de calcular la probabilidad de que 3030 personas cuyos votos son independientes (se supone) y que tienen dos opciones (no contamos abstenciones, varía poco). Pero no hubo caso, seguían insistiendo que estaba mal. Unos con fórmulas equivocadas, otros asegurando que hubo tongo y conspiraciones varias. Y otros que si hubiese sido impar el nḿero de votantes el empate es imposible (¡gran observación! :roll:).
Por supuesto que cuando calculas probabilidades te ciñes a unos supuestos, en este caso son muy simples:
- Son 3030 votos contabilizados, cada uno puede ser sí o no (o 0 y 1).
- Un empate se da cuando hay igual número de síes (1) que de noes (0).
Hay varias formas equivalentes de razonarlo:
- Probabilística: Se tiran 3030 monedas, como son sucesos independientes da igual si lanzas las 3030 a la vez o repites 3030 lanzamientos con la misma moneda. ¿Cuál es la probabilidad de que salgan 1515 caras y 1515 cruces?
- La (informática) de contar: Como la decisión es binaria, hay 2^3030 dígitos binarios diferentes que representan a la votación (o un número de 3030 bits), ¿cuántas combinaciones hay de números de 3030 bits cuyo número de 0 y 1 sean iguales? Sabiendo eso la probabilidad es sencillamente ese número de combinaciones dividido por el total (2^3030).
En ambos casos la solución es igual. El número de combinaciones posibles para monedas de dos caras – o números de 2 bits- con el coeficiente binomial para este caso es igual a binomial(3030, 1515).
Ese resultado enorme indica la cantidad de combinaciones posibles para que salgan 1515 síes (o 1) y 1515 noes (o 0) sobre un conjunto de 3030 elementos. Entonces la probabilidad de que salga un empate de las 2^3030 combinaciones posibles en total es igual a binomial(3030, 1515)/2^3030 = 0.0144938216980724… o aproximadamente: 1.44%
Es decir, la probabilidad de que ocurra un empate considerando votos independientes y equiprobables no es tan baja. De hecho es la más alta de cualquier otro resultado individual (que no con el total, la probabilidad de que no sea empate es 100% – 1.44% = 98.56%). Podéis probarlo fácil, por ejemplo de que hayan salido 1500 de síes (o noes) y 1530 de lo contrario.
Este es el punto, la probabilidad empate no es despreciable o «improbable» (sic) como aseguraban hasta matemáticos. Tampoco es 1/3030, ni 1/3031, ni 1/3029 como aseguraban otros.
A pesar que expliqué en una serie larga de tuits seguían insistiendo en que estaba mal, o que no consideraba conspiraciones. Lo siento, pero la pregunta es cuál era la probabilidad de que ocurra con votos independientes y equiprobables… que es como toca calcular para casos como este.
De todas formas, dado que las elecciones anteriores ya estaban muy empatadas la probabilidad de empate es aún mayor (podéis jugar cambiando las cifras de n y k en los enlaces anteriores). Esta probabilidad mayor puede salir tanto con fórmulas frecuentistas como con Bayes. Otros argumentan que hay que considerar votos en blanco, los resultados no cambiarán tanto e incluso aumentarán porque n será menor y el 2^n decrecerá más rápido.
Insisto en el fondo de la cuestión: la probabilidad de un empate no es tan baja como afirmaban muchos. Las conspiranoias o fraude no entran en el cálculo, no podemos presuponer (ni tenemos datos) que los votos secretos en la misma elección no eran independientes entre sí. Con esta excusa cualquier pregunta de probabilidades no tendría sentido ya que cualquier respuesta o aproximación será errónea con una probabilidad del 100% 😉
Aún más, si no creéis en las fórmulas, podéis probar simulando las votaciones con este pequeño programa en Python que simula 3030 votaciones binarias. Podéis ver que los resultados convergen con mayor número de «votaciones».
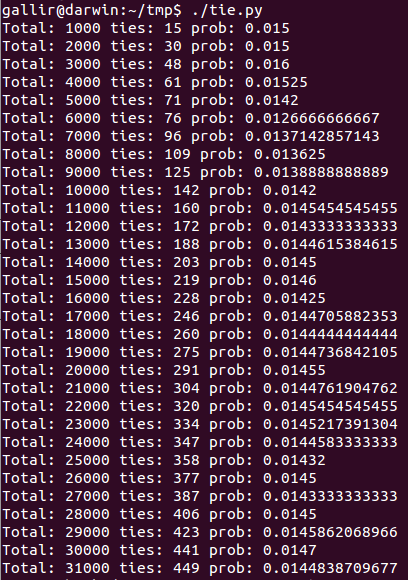
Pues mira, coincide la fórmula, la explicación y la simulación pura y dura.
PS: No pasa nada que matemáticos y economistas no se acuerden de probabilidades y combinatorias de primero de carrera, lo vergonzoso es que antes de desinformar con fórmulas erróneas no lo hayan verificado o probado con casos sencillos para asegurarse. Es su profesión y sus lectores les otorgan autoridad, collons.
PS2: Me pasan una gráfica de la distribución hecha en Excel, se observa bien la probabilidad de cada resultado individual y que. en general, los resultados cercanos al empate tienen mayor probabilidad.
PS3: Por supuesto, con votos impares el empate idéntico es imposible pero la distribución es la misma, habrá dos resultados con la misma probabilidad.
PS4: Ojo, no estoy asegurando que no hubo pucherazo, solo que no se puede inferir por probabilidades, tal como aseguraron muchos (¡incluso matemáticos y doctores de la cosa!).

Si se me permite introducir otro tema distinto de anumerismo de probabilidades en Cataluña, el otro día tiré en el nótame una observación sobre la probabilidad errónea de la publicidad de la lotería catalana:
https://www.meneame.net/notame/2309316
@lvps1000vm
Pues tienes razón, la probabilidad es un 25% más alta.
Pingback: O empate na CUP devolve a pelota ao tellado de JpS | Contradiscurso
Pingback: La CUP y probabilidades: para cuñadear, aprende matemáticas - Communia
«Es decir, la probabilidad de que ocurra un empate considerando votos independientes y equiprobables no es tan baja.» Ya, bueno, pues no te preocupes… Cuando haya una votación con votos independientes, equiprobables y binarios ya te llamaremos para que nos refresques el método. Lo digo porque esto no es un caso teórico… Aquí te están pidiendo el modelo descriptivo de una votación real celebrada hoy, con cinco opciones posibles (sí, no, voto nulo, voto en blanco, abstención), agregaciones de voto y condicionantes varios. El modelo probabilístico, estadístico y sociológico a aplicar es la releche en verso, pero tú tranquilo. Di que los demás somos tontos, altera el enunciado del problema a conveniencia y quédate con esto porque, como cualquier meneante medio sabe, cocinar los votos es malvada manipulación pepera, y cualquier corrección o ponderación se queda en pañales ante una socorrida media estadística. Y, naturalmente, las muestras importan poco. En fin… esto es como si te pidieran la distancia de frenado dw un coche concreto en unas circunstancias concretas, y tú respondieras que tienes una bonita fórmula que lo calcula sin tener en cuenta el rozamiento, la humedad, y la velocidad del aire. Pero, ¡eh! No voy a exigirle a un informático que entienda de sociología, pero sí que no vaya de listillo y perdonavidas por el mundo.
1,45%.
No soy matemático, confío en tu sapiencia y aplaudo la celeridad en publicarlo. Pero no puedo evitar ofrecerte alguna información que quizá pases por alto.
Estuve en la asamblea de la CUP. En los resultados de las dos primeras votaciones se nos ofrecieron por megafonía datos de:
1- votantes presentes
2- votos emitidos
3- votos nulos (y su porcentaje)
4 -votos en blanco (y su porcentaje)
5 -votos a cada una de las opciones (y sus porcentajes).
En cada votación variaba el número de presentes y el de emitidos. Es normal porque la primera votación se hizo a las 13h pero no se cerraron las inscripciones hasta las 16h con lo que aumentó el número de presentes en el recinto. Además siempre hay algunos que se ausentan o se abstienen. En la primera votación hubo 3004 votos totales emitidos y en la segunda 3042, una diferencia de 38 emitidos con 71 presentes más.
Sin embargo, al dar los resultados de la última votación no se mencionaron en ningún momento los presentes, los emitidos, los nulos ni los blancos (respecto a estos dos últimos ya habían avisado previamente que en la última votación no se computarían, sin especificar el motivo). Al final sólo se informó escuetamente que había un empate a 1515.
Lo digo para advertirte de que tus cálculos parten de la SUPOSICIÓN de que los emitidos válidos son 3030, pero no tenemos ninguna certeza al respecto. Por supuesto tu porcentaje del 1,44% es aproximadísimo y no variaría mucho de tener los datos omitidos por la organización (salvo que fueran impares, claro está).
La primera pregunta es: ¿por qué los omitieron?
La segunda pregunta es política. Si el reglamento establecía que se votaría hasta que una de las opciones superase el 50%, aunque fuera por un voto … porqué no hubo una cuarta votación?
En sus palabras finales Anna Gabriel, líder del sector anti-Mas, dijo que se había producido un empate técnico, cuando en realidad es un empate aritmético. Sorprende porque es abogada y domina el lenguaje. Quizá un desliz revelador, un acto fallido. Como el acto en su conjunto.
En todos los ejemplos que has puesto, se asume que la opinión de la gente sigue una distribución uniforme discreta, ademas de lo que has descrito de que sean independientes y dos opciones. Y claro, sale una probabilidad «alta». Lógicamente habrá algunos votantes que sean defensores del sí y otros que defiendan el no, pero se ha asumido que de media la opinión general es neutra. A mi me parece que es una asunción fuerte.
Si se asume una distribución de Bernuilli un poco descentrada, las probabilidades bajan mucho (por ejemplo 55-45).
Por su actualidad me ha parecido un a entrada excelente. Muchas gracias Ricardo
PS: has pensado en hacerte político? 😁😁
Una pequeña observación: creo que es más apropiado redondear que truncar, por lo que 0.0144938216980724 (0.01449,,,) sería aproximadamente 1,45% y no 1,44%
Y ahora viene el biologo friki a decir por que lo que se dice aqui no es correcto, y por que la probabilidad de empate no es 1,44%.
En primer lugar, en una binomial se toman sucesos independientes. Es decir, que cada votante no deberia tener nada que ver con el otro. Eso no es cierto en este caso, ya que en este tipo de actos, los votantes hablan entre si, interaccionan, y se intentan convencer cada cual de su resultado. Como ejemplo: SI en una votacion esta clarisimo que va a salir el SI, los partidarios del NO podrian callarse por verguenza.
Ademas cuando se usa una binomial, se asume que los dos resultados posibles (en este caso » si» o «no») tienen siempre la misma probabilidad de darse en cada repeticion, y que esta es conocida.
En una votacion existen multitud de factores que influyen en el voto de las personas. Tantos que no sabemos calcularlos, cierto, pero existen. (La economia del pais, la influencia de la prensa, la tasa de paro, incluso influyen cosas como si ese dia hace mucho calor y eso pone de peor humor a la gente).
En definitiva, el voto de cada persona no se decide al 50% «si» o «no», sino que cada voto esta determinado por miles de eventos que no podemos calcular, que cada persona integra dando su resultado individual.
En definitiva, en una votacion, los votos no son ni independientes, ni sabemos la probabilidad de que se decanten de un lado o de otro, ni esta es igual en cada votante.
Por eso no se puede usar una binomial para calcular la probabilidad del resultado.
Hola
Quizá lo que usted está calculando es más bien la entropía de la asamblea, es decir, el punto de equilibrio del sistema al que se llegaría a través de un número muy alto de modificaciones aleatorias de los votos individuales, en un proceso continuo de votaciones a lo largo del tiempo.
Un saludo.
Cuando un dedo apunta al cielo…
Viendo los resultados de las dos votaciones anteriores, se ve bastante claro que la mayoría de gente tenía clara la opción a votar. El número de votos que oscilaban entre las dos opciones era de unos 100 o 200. Utilizando esto como n en la distribución, las probabilidades son aun mayores.
Saludos.
Pingback: No, la CUP no amañó la votación | Enchufa2
Respondiendo a Francesc, sin poder aportar pruebas firmes, esta mañana desayunando en el bar, ha entrado una militante de la CUP y se ha sentado en la mesa de atras donde ya estaban dos asistentes en la assamblea de ayer. Ésta les pregunta por el empate a lo que responden que el si gano por 5 o 6 votos y no se puede decidir por tan poco asi que es empate….#manipulaCUP
Gracias Ricardo por el artículo, que me parece acertado a partir de las suposiciones que has hecho.
Sin embargo, creo que precisamente estas suposiciones son las problematicas. En resumen, «si se supone que la probabilidad de voto afimativo es 0.5, entonces la configuración de empate es la más probable y no neligible». Eso parece razonable. Pero yo creo que el problema no es ese. Asumes que la probabilidad de voto es exactamente de 0.5, pero eso lo supones porque el resultado ha sido empate! Estas usando los resultados para definir las condiciones iniciales. Eso no creo que sea correcto. El problema deberia formularse como ¿Cual es la probabilidad de que 3030 votos binarios empaten sin ninguna suposición a priori sobre la probabilidad de voto? Y ahí la probabilidad es mucho más baja y es por eso que sorprende de que 3030 votos empaten.
Alfonso, lo que se ha asumido de primeras es que la distribución de la variable voto a favor de Mas o en contra es una Bernoulli. Sin tener más información se supone que el voto es neutro (o aleatorio) y que por lo tanto la probabilidad es p. A partir de ahí el número de votos a favor de Mas (o en contra) es una binomial con parámetros p=0.5 y n= 3030 (el número de votos emitidos, por simplicidad no se cuentan los votos nulos y las abstenciones). Esta probabilidad, para el que tenga curiosidad, se puede calcular en EXCEL con la fórmula DISTR.BINOM.N.
Otro tema es que, tal y como se ha comentado, faltan datos y suena bastante sospechoso que en la votación final con un empate no se den todos los resultados.
La conclusión es que un empate, aunque poco probable, es posible. Si añadimos otros factores (políticos) el tema suena bastante mal.
Si nos ponemos exquisitos,… «Podéis ver que los resultados convergen con mayor número de ‘votaciones'» En esto quizá tenga algo que ver que Python y Excel generan números «pseudo-aleatorios» con algoritmos cuyos requisitos suelen ser que den resultados distribuidos de esa manera. Por lo demás, la explicación impecable
¿Y podrías hacer los cálculos de las probabilidades de empate acumuladas en cada ronda sabiendo los resultados de las opciones A y B (sin contar nulos ni blancos) en la primera y segunda operación?
estas equivocado, ya que tomas cada voto como un lanzamiento de moneda al aire, dando iguales posibilidades al si y al no, con lo cual tiende a equilibrarse, pero es falsa, ya que cada voto no tiene las mismas probabilidades (leñe, para eso se vota, porque se desconocen, si no saldría empate de antemano).
partiendo de que hay factores, muchos, múltiples, tantos que son imposibles de calcular, que cambian la probabilidad hacia el si o el no, el hecho de que todos esos factores se alineen para dar un 50% exacto es muy extraño.
te pongo un ejemplo, les das a elegir que comer a 3030 personas entre tarta o mierda de perro. según tu ejemplo tendría que salir 50% o aproximarse y que 1515 personas o casi elijirian para comer mierda de perro y ese sería el resultado mas probable. Como ves, algo falla en tu razonamiento.
3030 votantes. Empezamos con los posibles resultados:
0 sí, 3030 no; 1 sí, 3029 no; 2 sí, 3028 no; … ; 3030 si, 0 no
Total, 3030 combinaciones. Probabilidad de 1515 sí y 1515 no: 1/3030*100=0.033%. Cualquier resultado concreto es igualmente probable, pero tú dices además que el empate es más probable que cualquier otro resultado, lo que también es falso.
Yo usé la libreria Lea en python, hace el calculo exacto
https://bitbucket.org/piedenis/lea
Reformulando la pregunta estadística: la probabilidad de un empate en votos = 16%
http://www.eldiario.es/piedrasdepapel/probable-empate-Asamblea-CUP_6_467263286.html
Otras consideraciones:
1. ¿Cuál es la probabilidad de obtener 3030 votos en la tercera ronda cuando se contabilizaron 3022 votos válidos en la segunda ronda?
Razonamiento intuitivo: muy probable que entre los 20 participantes restantes de la segunda ronda (14 votos en blanco y 6 nulos) surgieran 8 votos adicionales en la tercera ronda.
2. ¿Cuál es la probabilidad de obtener una diferencia de cero en la tercera ronda cuando la diferencia fue de 30 en la segunda, con 28 votos restantes favoreciendo a Más?
Razonamiento intuitivo: muy probable que los 8 votos adicionales cerrasen la brecha de 2 votos (5-3=2)
Refraseando la pregunta sociológica:
3. ¿Cuál es la probabilidad de manipulación de unos pocos votos para favorecer un «empate técnico» y así dejar en manos de la cúpula directiva el poder decisional, en vez de permitir que un margen mínimo decidiera el futuro de tantos?
Razonamiento intuitivo: muy probable.
JB
Con il tutto respecto, el planteamiento que hace el sr. Lucas es precisamente el que hice yo. Por qué es erróneo, señor Gallir?
Reciba un cordial saludete.
Este es un post cuñado.
Lo es porque hace afirmaciones categóricas «LA probabilidad ES» basándose en un modelo absurdamente simple para describir la realidad. Pero sobre todo, por no dejar claras las asunciones que se hacen para obtener el resultado. El cálculo solo es cierto si cada uno de los votantes tira una moneda al aire para decidir su voto (o usa un procedimiento similar, aleatorio e independiente).
¿Es esto una buena aproximación? Como siempre, la respuesta depende de del nivel de precisión que queramos. Quizá sea un buen modelo para demostrar que una aproximación aun peor (todos los resultados son equiprobables) es aun peor. Pero desde luego, no es suficiente para afirmar que esa es LA probabilidad, y que cualquiera que diga lo contrario se equivoca (por «traducirlo» suavemente, pero con una dosis extra de cuñadismo en realidad). Alguien tan puntilloso con lo que escriben los demás debería estar a la altura de sus estándares 😉 .
Insisto en que el problema no es que no plantea un modelo sociológico complicado con teoría de redes, sino que no deja claro que es un cálculo basado en asunciones muy discutibles (como querer explicar el funcionamiento de un avión asumiendo que la densidad del aire es cero). Hubiera sido mucho más valioso si hubiese dejado claro qué asunciones se hacen, en lugar de una diatriba sobre que ningún problema de probabilidades tiene una solución exacta (no; ningún problema en ciencias naturales y mucho menos en ciencias sociales tiene una solución exacta, y precísamente por eso hay que dejar claro lo que se asume para cada cálculo). Mucho más claro aquí:
http://www.eldiario.es/piedrasdepapel/probable-empate-Asamblea-CUP_6_467263286.html
No se porque algunos decís que el voto de cada persona no es como tirar una moneda al aire, insinuando que la probabilidad de salir cara o cruz es del 50%.
Estáis haciendo un calculo DEMASIADO SIMPLISTA del lanzamiento de una moneda.
– Las monedas no son perfectamente simétricas, así que pueden tener un lado que pese más, por ejemplo, haciendo que la probabilidad cambie.
– Ademas puede existir intervención divina, ya que no podemos asegurar al 100% que ningún dios exista.
– La moneda puede tener dos caras, o dos cruces
– El que tira la moneda puede hacer trampas, o simplemente puede que se confunda al decir el resultado.
– Etc etc
Pingback: La CUP y la binomial - Naukas
a partir de los resultados de la 2a votación, se podría hacer una trinomial equiprobable (si, no, abstención) entre los 20 votos que no estan claros. Hay 10 posibles empates (1512,1513,…,1521) . La probabilidad de ALGÚN empate es del 9.36%.
esto condicionado a los resultados de la 2a votación claro.
La explicación matemática, impecable. Efectivamente parte de la base de que los votos son independientes entre sí y que ambas opciones eran igualmente probables. No, en este caso no puede incluirse la opción de comer mierda de perro, queda excluido de la premisa inicial. Sin embargo es un «vicio» intentar un cálculo de probabilidades, cuando las premisas iniciales son definitivamente falsas. La estadística permite hacer ciertas inferencias cuando el muestreo es «correcto», aunque en la práctica un muestreo «correcto» es prácticamente imposible. Pretender aplicar probabilidad a este caso queda totalmente fuera de lugar, pero permite entender que el resultado no es un «imposible».
Los que cuentan que hay solo 1 posibilidad de «1 sí, 3029 no», van equivocados, porque en este modelo en que cada voto es «independiente» y «equiprobable» hay exactamente 3030 casos de «1 sí, 3029 no».
Si es muy cuestionable el uso de estadísticas (por mucho que la palabra venga del «estudio del estado»), ya que las premisas de independencia que requiere el axioma fundamental de la estadística no se cumplen (ni tan siquiera las de muestreo), mucho menos puede aplicarse probabilidad a este caso, pero «a posteriori», sirve para justificar que no es un «imposible», o mejor dicho, para rebatir a aquellos que usan argumentos pseudomatemáticos para afirmar que es «imposible».
Lo malo de los modelos matemáticos simplificados es que a veces se apartan bastante de la realidad que intentan modelar. Recuerdo un chiste que se atribuía no a los matemáticos sino a sus primos los físicos: ¿que altura promedio crece anualmente un pino? Y el físico respondía: para una primera aproximación al problema consideremos un pino esférico y de masa nula.
yo entiendo que la realidad desmiente que las votos no están conectados, porque hay muchas votaciones a dos resultados y con muchos votantes y no se da casi nunca empate. por eso se hacen campañas para influir en lo que se vota y en las distintas tertulias y conversaciones. No conozco segundas vueltas que se tenga que repetir la votacion, los humanos no nos ajustamos a la campana de Gauss, cuando nos interesa, no lo hacen los imanes que se acoplan con lineal simpleza. Entiendo que el resultado que se presenta se dará cuando las personas que votan no se relacionan y son sujetos verdaderamente «independientes». Ademas a los que cuentan les puede interesar más votaciones para salir mas veces en la TV. es decir el que cuenta no es independiente, tampoco.
Definiendo una probabilidad individual constante de 0,5/0.5 está claro que el resultado con mayor probabilidad (1.44%) es el empate, aunque es muchísimo más probable (98.56%) que el resultado sea cualquier otro. De la misma forma, definiendo otra probabilidad individual cualquiera, por ejemplo 0.4/0.6 obtendríamos otro valor del resultado con una probabilidad mucho más alta que el resto. Es decir, dar por conocida esa probabilidad individual es casi tanto como conocer el resultado. Así, siendo el problema precisamente que no conocemos esa probabilidad individual, no me parece descabellado considerar, como hace Lucas, que todos los resultados son equiprobables. Otras opciones intermedias podrían considerar probabilidades condicionadas en función de las votaciones anteriores, pero en cualquier caso, el resultado con empate puede considerarse altamente inprobable.
Yo lo he hecho de otra forma. De esos 2^3030 formas posibles de realizar la votación, queremos el caso de que haya 1515 síes y 1515 noes. Este caso puede darse de muchas formas, pero serían las permutaciones de 3030 elementos donde el sí se repite 1515 veces y el no 1515 veces, estos es 3030!/1515!1515! Que serían los casos favorables. Por último divido entre los 2^3030 casos posibles y multplico por 100 para hallar el porcentaje. Lo hice así y me salió lo mismo, pero no se si el razonamiento es el correcto
Por cierto pero ya somos detallistas decirte que se dice buscar tres pies al gato.
Dado que lo que mosquea a la gente es el empate y este se da en la tercera votación, ¿por qué no plantear el problema como la probabilidad de empate en la tercera votación asumiendo que los que en la segunda votación votaron a favor de facilitar la investidura de Mas (opciones A y C) y los que votaron en contra mantuvieron su voto en la tercera votación?
Asumir este supuesto creo que no está muy alejado de la realidad (desde luego está más cercano a pensar que en la última votación todos volvieron a reconsiderar su voto), a esas alturas la inmensa mayoría del voto era fijo, teniendo en cuenta esto, podemos hacer una binomial con P=0,5 con los votos en blanco y nulos, calculando la probabilidad de que esos votos se repartiesen provocando el empate.
Si aceptamos una probabilidad individual de 0,5/0,5, el resultado más probable (con probabilidad 1,44%) es el empate (aunque es muchísimo más probable, 98,56%, que no haya empate) y el resto de la probabilidad se concentra fuertemente alrededor de ese resultado, como se observa en el gráfico publicado más arriba. De la misma forma, si consideramos otra probabilidad individual, por ejemplo 0,6/0,4 tendremos otro resultado alrededor del cual se concentrará mucha más probabilidad que en cualquier otro. Por tanto, conocida la probabilidad individual podemos decir que casi sabemos cuál será el resultado y casi no haría falta votar.
Pero el problema está precisamente en que no conocemos cuál es esa probabilidad individual. Por eso creo que considerar todos los resultados como equiprobables, como dice Lucas (y muchos otros) no es tan descabellado. Se podrían considerar situaciones intermedias, por ejemplo atendiendo a la probabilidad condicionada a los resultados de las votaciones anteriores, pero en cualquier caso puede considerarse que el resultado en empate era altamente improbable.
Un punto de vista algo distinto. Los dirigentes de la CUP (o lo que sean, consejo político, los que evaluaron el resultado …) pueden ver la votación como un experimento estadístico para ver cómo aprecian los militantes la idea de votar o no votar a Mas. No voy a hacer números para no liar pero si la hipótesis estadística es «hay una división total y la mitad de los militantes están a favor y la otra mitad en contra» cualquier resultado del experimento con poca diferencia entre posturas confirmaría esa hipótesis. Es decir quedaría confirmada con 1515 contra 1515 pero también con 1500 contra 1520, en cualquier caso podría confirmar la hipótesis de que la militancia está dividida por igual entre ambas posturas (el sentido común también dice lo mismo). Luego de cara a presentar los resultados a la opinión pública puedo cocinarlos para decir que ha habido empate, no engaño a la militancia ni a la opinión pública, realmente estoy diciendo que hay un división muy equilibrada en la militancia. Esto es análogo a que haga un experimento tirando 3030 monedas fabricadas en una misma serie para intentar comprobar la hipótesis «es igual de probable que caigan en cara o en cruz», si el número de monedas que caen de cara es cercano al que caen de cruz podría concluir aplicando un test de hipótesis estadístico que es cierto que la probabilidad es la misma, con gran certeza (los test de hipótesis se fijan para certezas del 99%, 99,9% o lo que sea, ya digo que evito los cálculos pero espero que la idea esté clara)
Pingback: Probabilidad de empate en una votación… | Raiden.tk
La conclusión lógica es que las hipótesis de equiprobabilidad e/o independencia absoluta no se cumplen. A otra cosa.
Naturalmente, los agentes realizan apuestas respecto a las votaciones de las distintas facciones, y realimentan esta información en su sistema decisional, combinándolo con la utilidad esperada de los distintos resultados posibles. Es evidente que, en una situación de elevada incertidumbre, un resultado de empate presenta una utilidad mayor, por cuanto que implica demorar una decisión crítica frente a un adversario no cooperativo (el estado español), donde debe pagar una prima quien antes revele sus cartas. Por todo ello es natural, y casi inevitable, la coalescencia de la votación colectiva hacia el empate, incluso aunque fuera inconsciente o no explícita a priori. La pelota queda ahora en otro tejado.
Aplicar la probabilidad del 50% me parece realista (al fin y al cabo, asumiendo que no hay tongo, es lo que muestra el resultado). Además, en las votaciones anteriores no es muy diferente. En cualquier caso, la conclusión es discutible: que sea la opción más probable no tiene ninguna relevancia (además este tipo de titulares dan lugar a confusión, porque podría entenderse que es más probable el empate que un resultado sin empate), lo que se discute es si es despreciable o no. Y 1,44% no es despreciable, pero para mí es lo suficientemente baja para que huela a tongo…
Creo que las percepciones de la gente se enmarañan proporcionalmente al numero de elementos polemizadores, ocurre con todas las cosas, al final se crea una madeja enredada de «no creo», «si creo», «…no se», etc… y lo que queda es la punta de un hilo que asoma difusamente, que no merece la pena , buscarle las vueltas y que hace que cada cual vuelva la su quehacer cotidiano. Una pena, pero si es que hay culpables ellos tambien lo saben.
Veras, como «soy de Letras» no me preocupo el pensar en el resultado matemático de probabilidad de empate, pero vistos algunos comentarios en RR.SS leí algunos y, sus conclusiones eran como la tuya. Cosa de la que no estoy seguro, creo que os dejais «la previa», la posibilidad de que el número de asistentes fuera impar, quizás por que solo hay dos posibilidades (el 50%) y, creo, eso haría que la cifra de probabilidades de empate que os sale fuera también la mitad ¿lo habéis tenido en cuenta o es la percepción de un profano? Estos problemas entendidos desde la «simple» lógica suelen dar sorpresas; como cuando preguntas a «cualquiera» que posibilidad tengo de sacar cara tirando una moneda al aire después de hacerlo 69 veces en que ha salido cruz, casi nadie dice el 50%…
No es técnicamente cierto que «…el empate es el resultado más probable de entre todos los posibles, con una probabilidad nada despreciable (1,44%).» Eso es así si comparamos el resultado del empate con el resto de combinaciones posibles. PERO lo que hemos de comparar es EMPATE Vs. NO EMPATE, y ahí, dando por cierto su cálculo del 1,44%, la realidad es que la probabilidad del NO EMPATE era del 98,56%.
Creo que el que no está preparado para las matemáticas de la CUP es usted, señor Arroyo
(PD: Dicho esto, también le diré que he disfrutado el artículo. Gracias)
Pingback: Más de CUP, el mal uso de probabilidades y un bayesiano | Ricardo Galli, de software
Respuesta a Ricardo Galli sobre los redondeos.
Si la primera cifra que se omite va de cero a cuatro, se redondea por defecto. Si es de cinco a nueve por exceso. Esa es la forma de redondeo más próxima al valor con más cifras. Así que 0.01445 ,,, sería aproximadamente 1,45%, pero 0.1444 sería 1,44% Simplemente truncar en todos los casos es una aproximación muy mala; por ejemplo, un informático que truncara de esa forma los ingresos de un banco y se ingresara en su cuenta particular los restos, acabaría con un capitalito.
Respuesta a Antonio Arnau. En la estadística tradicional, suponiendo que la moneda es perfecta y la forma de arrojarla aleatoria, cada suceso es independiente y en efecto la probabilidad de obtener cara en la tirada 70 cuando las 69 veces anteriores ha salido cruz, es el 50%. Pero con esos antecedentes la hipótesis más probable es que la moneda está trucada; quizás incluso los dos lados son cruces, así que lo razonable es apostar por otra cruz. Lo que sería absurdo sería apostar a que saldrá cara, «porque ya le toca».
En la estadística bayesiana se tienen en cuenta los resultados anteriores para refinar las predicciones. Por ejemplo, tras una primera tirada en la que ha salido cara, la apuesta más razonable para la siguiente tirada con la misma moneda es cara, porque eso está demostrado que puede salir, mientras que hasta que aparezca una cruz no está demostrado que pueda salir. La estadística tradicional hace muchas hipótesis no siempre expresas, que a veces no se cumplen.
Pingback: emprenyats | loflabiolaire
Pingback: ¿Por qué el empate de la CUP es más raro de lo que parece (y de lo que yo mismo digo)? – datanalytics
Por otro lado, asumir que es equiprobable que el número de votantes sea par o impar parece una hipótesis razonable. Y con esta hipótesis, la probabilidad de empate se reduce a la mitad…
Consideración adicional:
¿Por qué se añadió un voto al total de la tercera ronda?
[3043-3042=1]
Haz clic para acceder a 1451423156392.pdf
Otro enfoque estadístico:
P. ¿Cuál es la probabilidad de 1 voto nulo (o ninguno) en la tercera ronda cuando, de acuerdo a las dos rondas anteriores, se esperaban 5?
R. 4.1% (distribución Poisson acumulativa; la probabilidad de exactamente 1 voto nulo es 3.4%)
CONCLUSION: existe una fundada sospecha de que se amañó el resultado de la votación para producir un «empate técnico» que reflejara la realidad de una equivalencia estadística, a pesar de que en el juego democrático se puede ganar por sólo un voto. JB